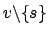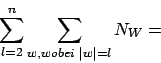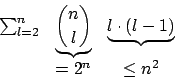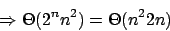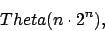Unterabschnitte
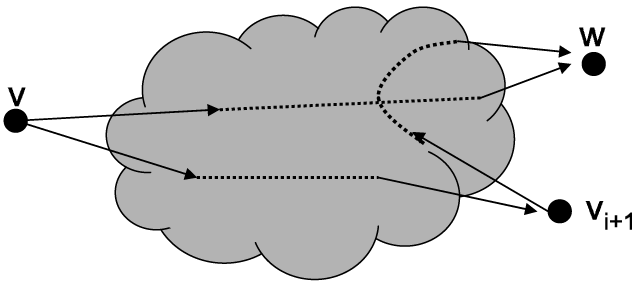
Die Idee dieses Algorithmusses ist es, daß für jeden Weg zu einem Knoten geprüft wird, ob er kürzer ist, wenn man direkt geht oder wenn man schon durch eine vorberechnete Menge D geht. Wird in der Menge D ein Knoten eingefügt, so wird versucht für jeden Knoten zu jedem Knoten einen Weg zu finden, der über diesen Knoten kürzer ist.
:
| |
 |
 |
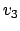 |
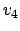 |
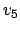 |
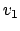 |
0 |
3 |
8 |
 |
-4 |
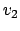 |
 |
0 |
 |
1 |
7 |
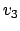 |
 |
4 |
0 |
 |
 |
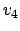 |
2 |
 |
-5 |
0 |
 |
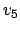 |
 |
 |
 |
6 |
0 |
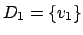
:
| |
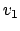 |
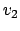 |
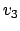 |
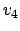 |
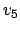 |
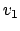 |
0 |
3 |
8 |
 |
-4 |
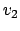 |
 |
0 |
 |
1 |
7 |
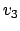 |
 |
4 |
0 |
 |
 |
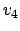 |
2 |
5 |
-5 |
0 |
-2 |
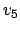 |
 |
 |
 |
6 |
0 |
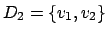
:
| |
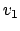 |
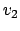 |
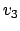 |
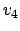 |
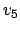 |
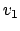 |
0 |
3 |
8 |
4 |
-4 |
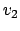 |
 |
0 |
 |
1 |
7 |
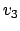 |
 |
4 |
0 |
5 |
11 |
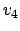 |
2 |
5 |
-5 |
0 |
-2 |
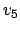 |
 |
 |
 |
6 |
0 |
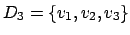
:
| |
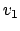 |
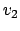 |
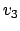 |
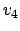 |
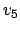 |
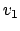 |
0 |
3 |
8 |
4 |
-4 |
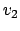 |
 |
0 |
 |
1 |
7 |
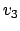 |
 |
4 |
0 |
5 |
11 |
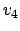 |
2 |
-1 |
-5 |
0 |
-2 |
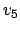 |
 |
 |
 |
6 |
0 |
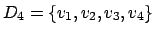
:
| |
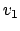 |
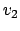 |
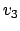 |
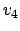 |
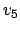 |
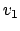 |
0 |
3 |
-1 |
4 |
-4 |
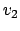 |
3 |
0 |
-4 |
1 |
-1 |
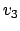 |
7 |
4 |
0 |
5 |
3 |
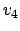 |
2 |
-1 |
-5 |
0 |
-2 |
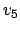 |
8 |
5 |
1 |
6 |
0 |
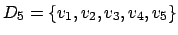
:
| |
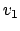 |
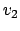 |
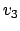 |
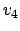 |
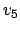 |
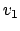 |
0 |
1 |
-3 |
2 |
-4 |
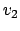 |
3 |
0 |
-4 |
1 |
-1 |
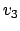 |
7 |
4 |
0 |
5 |
3 |
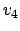 |
2 |
-1 |
-5 |
0 |
-2 |
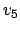 |
8 |
5 |
1 |
6 |
0 |
Im Graphen dürfen keine negativen Zyklen vorkommen. Dann werden Pfade gebildet, die unendlich klein sind und das schafft dieser Algorithmus auch nicht.
Es reicht, wenn wir uns bei jeder Veränderung merken, über welchen Knoten wir die Kosten der Kante verändert haben. Dann können wir den Pfad rekursiv zurückverfolgen.
Beim Warshall geht es nur um die Erreichbarkeitsanalyse. Wir verzichten deshalb auf Kantenkosten und legen nur eine Wahrheitstabelle an, die aussagt, ob ein Knoten von einem anderen aus erreichbar ist. Wir verwenden ein ähnliches Schema wie das des Floydalgorithmusses. Wir nehmen immer einen Knoten aus der noch nicht in D enthaltenen Menge mit hinzu und bestimmen für diesen für alle
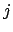
Knoten:
Das TSP (Traveling Salesman Problem - Problem eines Handlungsreisenden) ist das Problem den kürzesten Weg auf den Kanten durch alle Knoten zu finden, wobei jeder Knoten genau einmal besucht werden muß und auch demzufolge jede Kante nur einmal besucht werden darf. Das TSP-Problem ist das Problem einen
Hamiltonkreis auf dem Graphen zu finden.
Auch das TSP läßt sich mit Hilfe des dynamischen Programmierens effinzienter lösen. Das naive Verfahren hat die Laufzeit
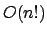
, da alle Permutationen ausprobiert werden müssen.
Die Laufzeit des TSP-Algorithmus läßt sich verringern, wenn man dynamisches Programmieren anwenden. Hierbei werden angefangen von allen zweielementigen Teilmengen die kürzesten Wege in allen Teilmengen gesucht, die dann letztendlich zu immer größeren Hamiltonwegen zusammengesetzt werden, bis letztendlich nur noch ein Hamiltonweg übrigbleibt
3. Das ganze läuft in einer Laufzeit von
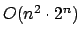
mit einem Platz von
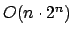
.
- Initialisieren kostet
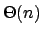 für jeden Knoten.
für jeden Knoten.
- Kosten pro
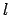 -elementige Teilmenge, die berechnet wird sind
-elementige Teilmenge, die berechnet wird sind 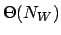
- Kosten summiert für alle Teilmengen
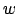 von
von
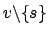
- Platzkomplexität ist
da für jede Teilmenge die Kosten des kürzesten Weg4es und der kürzeste Weg gespeichert werden müssen.
Fußnoten
- ... übrigbleibt3
- Genaueres sei hier nicht erklärt.
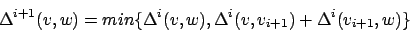
 :
:
 :
:
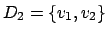 :
:
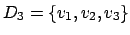 :
:
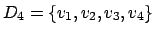 :
:
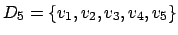 :
:
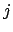 Knoten:
Knoten: 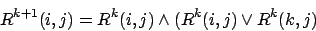
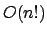 , da alle Permutationen ausprobiert werden müssen.
, da alle Permutationen ausprobiert werden müssen.
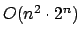 mit einem Platz von
mit einem Platz von
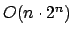 .
.

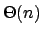 für jeden Knoten.
für jeden Knoten.
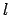 -elementige Teilmenge, die berechnet wird sind
-elementige Teilmenge, die berechnet wird sind 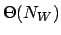
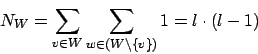
 von
von