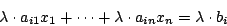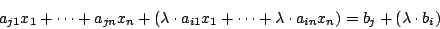Um zu zeigen, daß das Gauss-Verfahren ein lineares Gleichungssystem
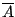
mit genau der gleichen Lösungsmenge wie das Gleichungssystem
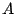
erzeugt, müssen wir beweisen, daß folgende Umformungen keinen Einfluß auf die Lösungsmenge haben:
- Vertauschen von Zeilen
- Multiplizieren von Zeilen mit
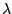 und anschließendes addieren auf eine andere Zeile
und anschließendes addieren auf eine andere Zeile
Zu
- Dies ist trivial. Das Vertauschen von Zeilen eines Gleichungssystems nimmt keinen Einfluß auf die Lösungsmenge, da die Reihenfolge egal ist.
- Wir betrachten zwei Zeilen des Gleichungssystems, da Umformungen nur mit Hilfe dieser beiden Zeilen stattfinden. Die anderen Zeilen bleiben unberührt und die Lösungsmenge wird nicht verändert:
Eine Multiplikation mit 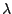 der (1)-Zeile verändert an der Lösungsmenge nichts, da man
der (1)-Zeile verändert an der Lösungsmenge nichts, da man 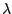 wieder kürzen kann:
wieder kürzen kann:
Addiert man nun die multiplizierte Zeile (1) zu der Zeile (2) wie folgt
An der Lösungsmenge ändert sich wiederum nichts, da man eine Gleichung hinzuaddiert, die auf beiden Seiten gleiche Anteile hinzugibt. Dies könnte wiederum gekürzt werden und wir hätten wieder die Ausgangsgleichung.
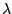 und anschließendes addieren auf eine andere Zeile
und anschließendes addieren auf eine andere Zeile

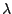 der (1)-Zeile verändert an der Lösungsmenge nichts, da man
der (1)-Zeile verändert an der Lösungsmenge nichts, da man 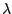 wieder kürzen kann:
wieder kürzen kann: