Nächste Seite: Der Vektorraum Aufwärts: Mengen mit Verknüpfungen Vorherige Seite: Polynomring Inhalt

Restklassen

Nun möchte ich gerne noch ein Beispiel für Körper vorstellen, die Restklassen von Primzahlen. Restklassen von Primzahlen kann man zu Körpern machen, indem man die Addition und Multiplikation auf ihnen definiert. Solche Körper heißen dann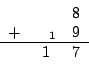 $\mathbb{F}_{p}$ also beispielsweise $\mathbb{F}_{7}$ für die Restklasse 7. In dem alltäglichen Leben rechnet man recht häufig mit der Restklasse

, zum Beispiel bei der schriftlichen Addition^2.2:

$\begin{displaymath}\begin {array}{ccc}&&8\\ +&\,\,\,\,\,_{1}&9\\ \hline&1&7\\ \end {array}\end{displaymath}$

Wir haben

und

addiert, wobei wir den Übertrag

nicht vergessen haben. Nun können wir den Übertrag weglassen und schreiben

$\begin{displaymath}8 \mbox{ mod }10 + 9 \mbox{ mod }10 \equiv 7 \mbox{ mod }10\end{displaymath}$

wobei ,,mod'' modulo bedeutet, also Rest der Division.
Ähnlich können wir auch andere Restklassen definieren. Statt durch

teilen wir beispielsweise durch

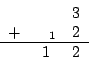
$\begin{displaymath}\begin {array}{ccc}&&3\\ +&\,\,\,\,\,_{1}&2\\ \hline&1&2\\ \end {array}\end{displaymath}$

Dazu können wir eine Additions und Multiplikationstabelle aufstellen:

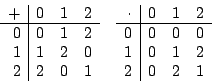
$\begin{displaymath}\begin{array}{cc}\begin{array}{r\vert ccc} +&0&1&2\\ \hline ... ...e 0&0&0&0\\ 1&0&1&2\\ 2&0&2&1\\ \end {array}\\ \end {array}\end{displaymath}$

Machen wir dasselbe noch einmal, diesmal für die Restklasse

$\begin{displaymath}\begin{array}{cc}\begin{array}{r\vert cccc} +&0&1&2&3\\ \hli... ...1&2&3\\ 2&0&2&0&2\\ 3&0&3&2&1\\ \end {array}\\ \end {array}\end{displaymath}$

Nun können wir die einzelnen Körperaxiome an dem zur Restklasse enventuell gehörenden Körper mit Hilfe der Wertetabellen überprüfen. Das Kommutativgesetz gilt, wenn die Tabellen an der Diagonalen spiegelsymetrisch sind. Das inverse Element existiert, wenn in jeder Spalte und Zeile der Tabelle jedes Element des Körpers einmal vorkommt. Das Nullelement existiert, wenn die

in jeder Spalte und Zeile vorkommt. Das Assoziativ und Distributivgesetz läßt sich an der Tabelle nicht so einfach ablesen.

Nachdem wir diese Anhaltspunkte haben, erkennen wir, dass der Körper $\mathbb{F}_{4}$ nicht existiert. Es wird gegen das inverse Element der Multiplikation verstoßen. Es gibt kein für $2\cdot x=1$ . Also kann man die Restklasse zu keinem Körper machen. Hingegen ist ein Körper $\mathbb{F}_{3}$ aus der Restklasse möglich, da kein Axiom verletzt ist: Wir sehen, dass Symmetrie und inverses Element sowie neutrales Element vorhanden sind. Ebenso sind auch bei näherem Nachprüfen Assoziativgesetze und Distributivgesetze gültig.

Wenn wir nun weiter forschen, so erkennen wir ein System darin, wann eine Restklasse zu einem Körper $\mathbb{F}_{p}$ . Das ist genau dann der Fall, wenn eine Primzahl ist. Dies zu beweisen wollen wir hier nicht ausführen.

Jedoch wollen wir zum Abschluss noch definieren, was eine Charakteristik ist und warum die Charakteristik eines beliebigen Körpers $\mathbb{K}$ immer eine Primzahl oder ist:

Definition: Charakteristik:
$\mathbb{K}$ sei ein Körper und sein neutrales Element der Multiplikation (Einselement). Für positive Zahlen verstehen wir unter $n\cdot 1$

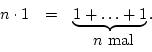
$\begin{displaymath}\begin {array}{ccc}n\cdot 1&=&\underbrace{1+\ldots+1}.\\ &&\mbox{$n$\ mal}\\ \end {array}\end{displaymath}$

Die Charakteristik des Körpers $\mathbb{K}$ ist definiert als

$\begin{displaymath}\mbox{char}\mathbb{K}=\left\{\begin {array}{ll}0&\mbox{wenn e... ...mbox{das kleinste $n$, so dass gilt $n1=0$}.\end {array}\right.\end{displaymath}$

Beweis:

ist immer eine Primzahl:
Sei $n\not=0$ (2.Fall der Definition). Wenn

keine Primzahl, dann zerfällt sie in Faktoren^2.3

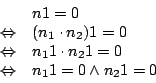
$\begin{displaymath} \begin {array}{ll} &n1=0\\ \Leftrightarrow&(n_{1}\cdot n_{2... ...}1=0\\ \Leftrightarrow&n_{1}1=0\wedge n_{2}1=0\\ \end {array}\end{displaymath}$

Wiederspruch. Da $n_{1}<n$ und $n_{2}<n$ müßte nun char $\mathbb{K}=n_{1}$ oder char $\mathbb{K}=n_{2}$ sein. Es ist aber char $\mathbb{K}$ =n und somit kann

nicht in Faktoren zerlegt werden, ist also eine Primzahl.

$\Box$

Aus der Schule kennen wir die wichtigen Körper der rationalen Zahlen $\mathbb{Q}$ der reellen Zahlen $\mathbb{R}$ und vielleicht auch noch der komplexen Zahlen $\mathbb{C}$ . All diese Körper haben die Charakteristik

. Es gibt noch weitere wichtige Mengen. Zum Beispiel die Menge $\mathbb{Z}$ , die Menge aller ganzen Zahlen. Diese ist leider nur eine kommutative Gruppe, da das inverse Element der Multiplikation fehlt. Das ist deshalb so, weil wir in dieser Menge keine Brüche haben. Die Menge $\mathbb{N}$ aller natürlichen Zahlen, sei nun

eingeschlossen oder nicht, ist leider gar nichts, noch nicht einmal eine Gruppe, da wir kein inverses Element der Addition haben; z.B. fehlt

für

, da es

nicht gibt.

Nächste Seite: Der Vektorraum Aufwärts: Mengen mit Verknüpfungen Vorherige Seite: Polynomring Inhalt