Unterabschnitte
Unterschiedliche Problemvarianten
Vorstellung mit Beispiel
Als Beispiel wird hier das CP20 genommen.- Entscheidungsproblem: Gibt es eine Lösung mit dem Wert
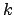 ? Beispiel: Gibt es eine Clique der Größe
? Beispiel: Gibt es eine Clique der Größe 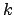 ?
?
- Optimierungsproblem Typ 1: Bestimme den Wert
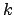 der optimalen Lösung Beispiel: Wieviele Knoten umfaßt die größte Clique im Graphen?
der optimalen Lösung Beispiel: Wieviele Knoten umfaßt die größte Clique im Graphen?
- Optimierungsproblem Typ 2: Gebe die optimale Lösung zurück! Beispiel: Rückgabe der Knoten der größtmöglichen Clique im Graphen
- Gibt es eine Rucksackfüllung mit dem Gewinn k?
- Was ist der Gewinn k einer optimalen Rucksackfüllung? (Gibt den maximalen erzielbaren Gewinn k zurück!)
- Welche Gewichte sind in der optimalen Rucksackfüllung enthalten?
Überführung ineinander am Beispiel des Cliquenproblems
Es sieht so aus, als ob dies drei völlig unterschiedliche Probleme seien. Dennoch snd sie in vielen Fällen gleichschwierig. Beim CP sind sie gleichschwierig. Wir zeigen dies21:- Es ist klar, daß man das Optimierungsproblem von Typ 2 auf Typ 1 zurückführen kann und Typ 1 auf das Entscheidungsproblem zurückgeführt werden kann. Dies tut man, indem man einfach ,,Teillösungen'' der zurückgegebenen Lösung zurückgibt.
- Man kann das Entscheidungsproblem in das Optimierungsproblem vom Typ 1 umwandeln, indem man das
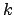 von
von 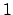 starten läßt und, solange das Entscheidungsproblem ,,JA'' zurückgibt, um 1 erhöht. Sobald wir ein ,,NEIN'' vom Entscheidungsproblem bekommen, wissen wir, daß das
starten läßt und, solange das Entscheidungsproblem ,,JA'' zurückgibt, um 1 erhöht. Sobald wir ein ,,NEIN'' vom Entscheidungsproblem bekommen, wissen wir, daß das 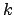 des ,,JA''-s davor die größte Clique ist22.
des ,,JA''-s davor die größte Clique ist22.
- Das Optimierungsproblem vom Typ 1 kann man in das Optimierungsproblem vom Typ 2 umwandeln, indem man den Graphen nimmt und immer eine Kante aus dem Graphen entfernt. Nachdem man diese entfernt hat, läßt man den Optimierungsproblemalgorithmus des Typs 1 noch einmal laufen. Gibt er immer noch das gleiche
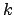 zurück, so hat man die Clique nicht zerstört, und man kann die Kante dauerhaft entfernt lassen. Wenn das
zurück, so hat man die Clique nicht zerstört, und man kann die Kante dauerhaft entfernt lassen. Wenn das 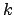 kleiner wird, wird die Kante wieder dem Graphen hinzugefügt und als ,,besucht'' markiert. Dies wird solange gemacht, bis alle Kanten im Graphen als ,,besucht'' markiert sind. Nun haben wir die Knoten der Clique.
kleiner wird, wird die Kante wieder dem Graphen hinzugefügt und als ,,besucht'' markiert. Dies wird solange gemacht, bis alle Kanten im Graphen als ,,besucht'' markiert sind. Nun haben wir die Knoten der Clique.
Fußnoten
- ... CP20
- Cliquenproblem
- ... dies21
- Hinweis: Für das RP ist nicht alles überführbar.
- ... ist22
- Dies folgt daraus, daß jede
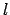 -er Clique auch eine
-er Clique auch eine 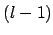 -er Clique ist.
-er Clique ist.