Unterabschnitte
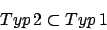
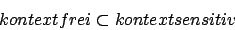
Bei Typ 2 darf auf der rechten Seite in jeder beliebigen Regel das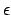 stehen. Bei Typ 1 jedoch nicht. Wir können jedoch jede kontextsensitive Grammatik in der die Regel
stehen. Bei Typ 1 jedoch nicht. Wir können jedoch jede kontextsensitive Grammatik in der die Regel 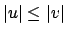 durch das
durch das 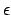 verletzt ist, in eine äquivalente regelkonforme Grammatik umformen.
verletzt ist, in eine äquivalente regelkonforme Grammatik umformen.
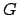 in eine äquivalente
in eine äquivalente 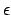 -freie CFG:
-freie CFG:
Markiert werden nacheinander folgende Nichtterminale (letztendlich alle):
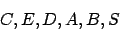
Wir streichen die Regel
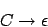
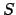 ist Element von
ist Element von 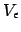 . Wir müssen ein Startsymbol
. Wir müssen ein Startsymbol 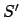 hinzufügen:
hinzufügen:
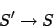
Folgende Regeln entstehen nun bei dem Durchlauf des Transformationsalgorithmusses:
Transformation um die ε-Freiheit bis auf S → ε in Typ 1 herzustellen
Es gibt eine kleine technische Panne beiBei Typ 2 darf auf der rechten Seite in jeder beliebigen Regel das
Algorithmus
Markierungsalgorithmus:- Markiere alle Non-Terminale
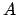 mit
mit
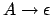
- Solange es Regeln gibt, so daß die rechte Seite aus lauter markierten Non-Terminalen besteht, markiere das Non-Terminal auf der linken Seite.
- Gebe alle markierten Non-Terminale als
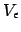 aus.
aus.
- Falls das Nonterminal
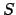 in irgendeiner Regel auf der rechten Seite vorkommt, füge
in irgendeiner Regel auf der rechten Seite vorkommt, füge
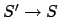 ein.
ein.
- Führe den oben beschriebenen Markierungsalgorithmus durch.
- Entferne alle Regeln
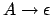 aus der Grammatik
aus der Grammatik
- Wenn
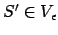 füge
füge
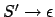 ein.
ein.
- Solange es eine Regel
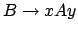 mit
mit 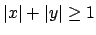 und
und
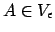 gibt, füge
gibt, füge
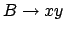 ein, wenn diese Regel noch nicht existiert.
ein, wenn diese Regel noch nicht existiert.
Beispiel
Transformation von folgender GrammatikWir streichen die Regel
Folgende Regeln entstehen nun bei dem Durchlauf des Transformationsalgorithmusses:
|
|
||
|
|
||
|
|
||
|
|
||