Wortproblem für Typ 0 und Typ 1 Sprachen
Das Wortproblem für Sprachen vom Typ 0 ist unentscheidbar.
Dies ist im wesentlichen eine Folgerung aus der Unentscheidbarkeit des Halteproblems.
Das Wortproblem für Sprachen vom Typ 1 ist 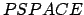 -vollständig.
-vollständig.
Wir können aufgrund dieser Erkenntnis ein Verfahren angeben, welchen Worstcaselaufzeit Sei
und
Wenn wir uns den Berechnungsbaum vorstellen, so ist
Algorithmus zur Berechnung, ob ein Wort
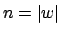
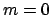
-
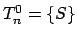
- Wiederhole
- Berechne
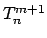
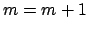
- Berechne
- Solange bis
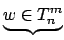
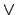
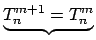
Wort enhalten Es kommen keine neuen Wörter mehr hinzu 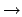 Wort nicht enhalten
Wort nicht enhalten