Unterabschnitte
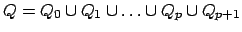 , wobei
, wobei 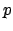 die Anzahl der Programmzeilen der Registermaschine ist. Die Zustandsmenge
die Anzahl der Programmzeilen der Registermaschine ist. Die Zustandsmenge 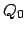 erzeugt die Ausgangskonfiguration auf den Bandzellen, die Zustandsmenge
erzeugt die Ausgangskonfiguration auf den Bandzellen, die Zustandsmenge 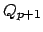 stellt die Ausgabe zur Verfügung.
stellt die Ausgabe zur Verfügung.
Die Turingmaschine verwendet nun 4 Bänder:
Wird nun ein Befehl, der in einer Programmzeile steht, abgearbeitet, wird folgendes gemacht (Am Beispiel von add 24):
24):
Jeder Befehl benötigt eine konstante Anzahl an Suchoperationen bzw. arithmetischen Operationen, die ausgeführt werden müssen. Diese laufen in polynomieller Zeit.
Es gilt
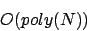
Für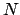 gilt
gilt
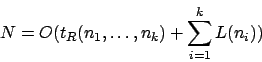
was darauf zurückzuführen ist, daß die Registermaschine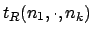 Zeit braucht und die Länge des Bandes
Zeit braucht und die Länge des Bandes
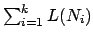 ist, über welches gespult wird.
ist, über welches gespult wird.
Insgesamt erhalten wir als Laufzeit der Simulation
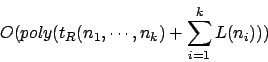
Insbesondere, wenn die Laufzeit der Registermaschine polynomiell beschränkt ist, gilt für die gesamte Simulation
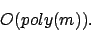
Die Übergangsfunktion wird simuliert, indem wir für jede partielle Funktion eine IF-Abfrage programmieren:
Wenn(Zustand=... und Zeichen=...)
dann{Zustand=...; Zeichen=...; Zeigerbewegung=...;}
1. Möglichkeit: Durch indirekte Adressierung
Man benutzt eine linksseitig beschränkte DTM. Diese ist äquivalent zu der unbeschränkten DTM.
Man kann nun die DTM mit Hilfe des ,,Semibandes'' simulieren.
Kosten:
Die Rechenzeit der DTM ansich ist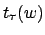 . Dabei werden maximal
. Dabei werden maximal 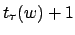 Bandquadrate besucht. Die Operanden der Registermaschinen-Befehle sind deshalb aus dem Bereich
Bandquadrate besucht. Die Operanden der Registermaschinen-Befehle sind deshalb aus dem Bereich
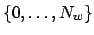 , wobei
, wobei
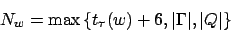
Somit kostet jeder Konfiguartionswechsel
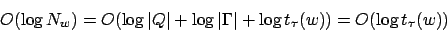
Es werden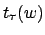 Konfigurationswechsel ausgeführt. Deshalb sind die Gesamtkosten für das logarithmische Kostenmaß:
Konfigurationswechsel ausgeführt. Deshalb sind die Gesamtkosten für das logarithmische Kostenmaß:
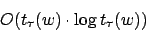
unter dem uniformen:
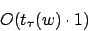
Hinzu kommen unter dem uniformen Kostenmaß
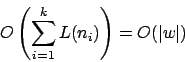
und unter dem logarithmischen Kostenmaß
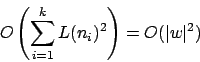
Schritte zur Erstellung der Ausgangskonfiguration.
Daraus folgt: Die gesamte Simulation läuft unter:
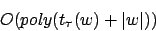
2. Möglichkeit: Mit zwei Stacks
Wir benutzen zwei Keller. Auf den einen tun wir den linken Teil des Bandes, der links vom Schreib/Lesekopf zu finden ist, auf den anderen den rechten Teil. Weiterhin benutzen wir eine Variable für die aktuelle Bandzelle9.
Wir können die Keller implementieren, indem wir Bitverschiebungen10 machen. Wir können einen Wert des Stacks durch die Basis mit Rest teilen und erhalten die oberste Zelle oder aber wir können eine Zelle auf den Stack schieben, indem wir den Wert des Stacks mit der Basis multiplizieren und den Wert der Zelle addieren:
Rauf:
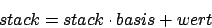
Runter:
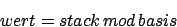
Auf Band 1 der universellen Turingmaschine steht die kodierte Turingmaschine und das darauf angewandte Eingabewort. Folgendermaßen kann man die Übergangsfunktion kodieren:
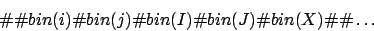
Auf Band 2 speichern wir den aktuellen Zustand. Auf Band 3 wird der aktuelle Bandinhalt gespeichert. Band 4 benutzen wir für Nebenrechnungen. Eine solche universelle Turingmaschine kann die eingegebene Turingmaschine simulieren.
- Simulation von Registermaschinen durch Turingmaschinen
- Simulation von Turingmaschinen durch Registermaschinen
- Simulation von Turingmaschinen mit Turingmaschinen - Universelle Turingmaschinen
Registermaschine ↔ Turingmaschine
Man kann eine Registermaschine mit einer Turingmaschine simulieren und umgekehrt. Hiermit führt man auch den Beweis, daß eine Registermaschine mit indirekter Adressierung die gleiche Mächtigkeit wie eine Registermaschine mit direkter Adressierung hat.Simulation von Registermaschinen durch Turingmaschinen
Die Zustandsmenge ist:Die Turingmaschine verwendet nun 4 Bänder:
| 1.Band | Eingabe |
| 2.Band | Registerbelegung der Form |
|
|
|
| 3.Band | Ausgabe |
| 4.Band | Nebenrechnungen |
- Auf Band 2 wird zuerst an die Stelle 24 gespult, dann wird an die Stelle gespult, wo der Wert aus der Registerzelle 24 hinzeigt. Dieser Wert wird ausgelesen und auf das Nebenrechnungsband (Band 4) gelegt.
- Der Akkumulator
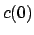 auf Band 2 wird mit dem Nebenrechnungsband bitweise addiert.
auf Band 2 wird mit dem Nebenrechnungsband bitweise addiert.
- Das Ergebnis wird zurück in den Akkumulator kopiert. Die Zustandsmenge wechselt in die nächste Zustandsmenge7:
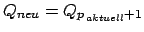 .
.
Jeder Befehl benötigt eine konstante Anzahl an Suchoperationen bzw. arithmetischen Operationen, die ausgeführt werden müssen. Diese laufen in polynomieller Zeit.
Es gilt
Für
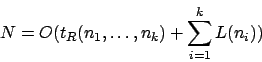
was darauf zurückzuführen ist, daß die Registermaschine
Insgesamt erhalten wir als Laufzeit der Simulation
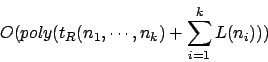
Insbesondere, wenn die Laufzeit der Registermaschine polynomiell beschränkt ist, gilt für die gesamte Simulation
Simulation von Turingmaschinen durch Registermaschinen
Allgemeiner TeilDie Übergangsfunktion wird simuliert, indem wir für jede partielle Funktion eine IF-Abfrage programmieren:
Wenn(Zustand=... und Zeichen=...)
dann{Zustand=...; Zeichen=...; Zeigerbewegung=...;}
1. Möglichkeit: Durch indirekte Adressierung
Man benutzt eine linksseitig beschränkte DTM. Diese ist äquivalent zu der unbeschränkten DTM.
| Register 1: | aktueller Zustand |
| Register 2: | Nummer des jeweils gelesenen Zeichens ( |
| dann geht es für das Bandalphabet |
|
| Register 3: | Position des Zeigers auf dem simulierten Band |
| Register 4: | Wird freigehalten für Nebenrechnungen |
| Register 5 und höher: | Das Band der Turingmaschine8 |
Kosten:
Die Rechenzeit der DTM ansich ist
Somit kostet jeder Konfiguartionswechsel
Es werden
unter dem uniformen:
Hinzu kommen unter dem uniformen Kostenmaß
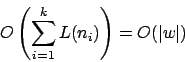
und unter dem logarithmischen Kostenmaß
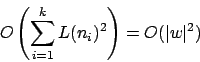
Schritte zur Erstellung der Ausgangskonfiguration.
Daraus folgt: Die gesamte Simulation läuft unter:
2. Möglichkeit: Mit zwei Stacks
Wir benutzen zwei Keller. Auf den einen tun wir den linken Teil des Bandes, der links vom Schreib/Lesekopf zu finden ist, auf den anderen den rechten Teil. Weiterhin benutzen wir eine Variable für die aktuelle Bandzelle9.
Wir können die Keller implementieren, indem wir Bitverschiebungen10 machen. Wir können einen Wert des Stacks durch die Basis mit Rest teilen und erhalten die oberste Zelle oder aber wir können eine Zelle auf den Stack schieben, indem wir den Wert des Stacks mit der Basis multiplizieren und den Wert der Zelle addieren:
Rauf:
Runter:
Simulation von Turingmaschinen mit Turingmaschinen - Universelle Turingmaschinen
Eine Turingmaschine kann man als ein einzelnes Wort kodieren. Universelle Turingmaschinen benutzen als Eingabe eine Turingmaschine, die sie simulieren.Auf Band 1 der universellen Turingmaschine steht die kodierte Turingmaschine und das darauf angewandte Eingabewort. Folgendermaßen kann man die Übergangsfunktion kodieren:
Auf Band 2 speichern wir den aktuellen Zustand. Auf Band 3 wird der aktuelle Bandinhalt gespeichert. Band 4 benutzen wir für Nebenrechnungen. Eine solche universelle Turingmaschine kann die eingegebene Turingmaschine simulieren.
Fußnoten
- ... Zustandsmenge7
- Sofern wir keine Gotobefehle haben
- ... Turingmaschine8
- Das Register
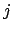 enthält die
enthält die 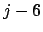 te Bandzelle
te Bandzelle
- ... Bandzelle9
- Alternativ kann man auch auf diese verzichten. Es gibt Implementierungen, die direkt mit der Variable vom Stack arbeiten.
- ... Bitverschiebungen10
- Im Binärsystem. In anderen Systemen verschieben wir um andere Basen.