Unterabschnitte
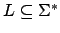 eine Sprache.
eine Sprache. 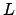 ist semientscheidbar, wenn es eine DTM
ist semientscheidbar, wenn es eine DTM 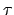 gibt, für die gilt
gibt, für die gilt
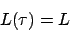
d.h. Für alle Worte der Sprache L akzeptiert die DTM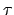 . Wenn die partielle charakteristische Funktion turingberechenbar ist, ist die Sprache semientscheidbar.
. Wenn die partielle charakteristische Funktion turingberechenbar ist, ist die Sprache semientscheidbar.
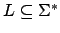 eine Sprache.
eine Sprache. 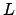 ist entscheidbar, wenn es eine DTM
ist entscheidbar, wenn es eine DTM 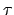 gibt, für die gilt
gibt, für die gilt
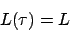
und für alle Worte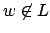 verwirft die DTM
verwirft die DTM 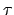 . Wenn die totale charakteristische Funktion turingberechenbar ist, ist die Sprache entscheidbar.
. Wenn die totale charakteristische Funktion turingberechenbar ist, ist die Sprache entscheidbar.
Nicht entscheidbar
Die Sprache
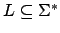 wird unentscheidbar genannt, wenn sie nicht entscheidbar ist, d.h. es gibt keine DTM
wird unentscheidbar genannt, wenn sie nicht entscheidbar ist, d.h. es gibt keine DTM 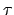 , die für alle
, die für alle 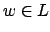 akzeptiert und für alle
akzeptiert und für alle 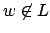 verwirft.
verwirft.
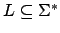 wird nicht semientscheidbar genannt, wenn es keine DTM gibt, für die gilt
wird nicht semientscheidbar genannt, wenn es keine DTM gibt, für die gilt 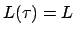 .
.
Entscheidbarkeit
Semientscheidbarkeit
Seid.h. Für alle Worte der Sprache L akzeptiert die DTM
Entscheidbarkeit
Seiund für alle Worte